Adaptive Cross Approximation (ACA)

In the computational scienes low rank approximations play a key role. It is well known that the best rank-\(k\) approximation in terms of either the spectral norm or the Frobenius norm is the truncated Singular Value Decomposition (Eckart-Young-Mirsky Theorem). However the SVD is expensive to compute, as such it is of interest to establish other ways of computing good low rank approximations.

The simplest these computational methods is the Adaptive Cross Approximation (ACA) which in simple terms is based on exact interpolation of \(k\) rows and columns. In the following visualization we choose rows \(r=\{2,4,7\}\) and columns \(c=\{1,3,6\}\)

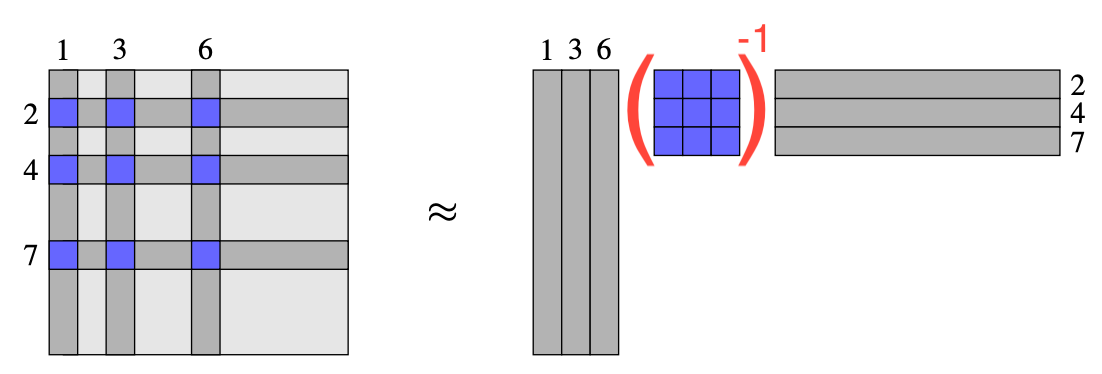
This picture is taken from ^[1]. A very solid introduction to Hiearchical Low-Rank Structures.

That the above expression perfectly interpolates the rows (\(r\)) and columns (\(c\)) of G be seen by looking at the following matrix

\[ G = \begin{bmatrix} \overline{G} & \overline{G}(:,c)\\ \overline{G}(r,:) & G(r,c)\end{bmatrix} \]

Now compute the approximation

\[\begin{aligned} G(:,c)G(r,c)^{-1}G(r,:) &= \begin{bmatrix}\overline{G}(:,c)\\ G(r,c)\end{bmatrix}G(r,c)^{-1}\begin{bmatrix}\overline{G}(r,:)& G(r,c)\end{bmatrix}\\ &= \begin{bmatrix}\overline{G}(:,c)\\ G(r,c)\end{bmatrix}\begin{bmatrix}G(r,c)^{-1}\overline{G}(r,:)& I\end{bmatrix}\\ &= \begin{bmatrix}\overline{G}(:,c)G(r,c)^{-1}\overline{G}(r,:) & \overline{G}(:,c)\\ \overline{G}(r,:) & G(r,c)\end{bmatrix}, \end{aligned}\]

from which the perfect interpolations of rows \(r\) and columns \(c\) and can be seen.

How do we choose the index sets?

While the ACA approach is easily explained we still need a way to pick the best rows and columns. Because we want to be able to use the ACA on matrices of sizes where the SVD is not feasible we want a heuristic approach that scales close to \(O(n)\).

Stopping criterion

\[ \|R_k\|_F \leq \epsilon \|A\|_F \]

\(\|A\|_F\) can not be computed. Instead use that \( A_k = UV^\top = \sum_{i=1}^k u_iv_i^\top \). So that

\[ \|A_k\|_F^2 = \|A_{k-1}\|_F^2 + \|u_k\|_2^2\|v_k\|_2^2 \sum_{i=1}^{k-1}u_k^\top u_iv_i^\top v_k. \]

Final stoppping criterion

\[ \|u_k\|_2\|v_k\| \leq \epsilon \|A_k\|_F \]

References

[1]	Ballani, Jonas, and Daniel Kressner. “Matrices with Hierarchical Low-Rank Structures.” Lecture Notes in Mathematics, vol. 2173, Springer Verlag, 2016, pp. 161–209, doi:10.1007/978-3-319-49887-4_3.