Mikkel Paltorp

Symmetric Extended Generator Representable Semiseparable Matrices

The following is a simple example of how the matrices found in SymSemiseparableMatrices.jl, can aid in efficiently computing smoothing splines.

Given \(n\) noisy observations

\[(t_i,y_i), \quad i=1,\dots, n\]

where \(y_i = f(t_i) + e_i\) and \(e_i\sim \mathcal{N}(0,\sigma^2)\). We aim to find the underlying function \(f\). For the smoothing spline regressions problem the view taken is that \(f\) minimizes the following functional

\[ \min\ \mathcal{J}_p(f) \equiv \frac{1}{n}\sum^n_i(y_i - f(x_i))^2 + \lambda \int_a^b |f^{(p)}(x)|^2\ \mathrm{d}x, \]

for some \(\lambda > 0\). This minimization problem can be viewed as a tradeoff between the interpolation of the data, described by average squared residual and the smoothness, described by the square integral of the \(p\)th derivative.

It can be shown that this problem is equivalent with solving the following QP

\[ \text{minimize}\ \frac{1}{n}\|y - (\Sigma c + Hd) \|_2^2 + \lambda c^\top\Sigma c \]

where \(H\in\mathbb{R}^{n\times p}\) with elements \(H_{i,j} = t_i^{j-1}/((j-1)!)\) and \(\Sigma \in\mathbb{R}^{n\times n}\) is a positive definite (kernel) matrix. As shown in (Anders & Chen 2020) \(\Sigma\) is rank-structured and have the following form

\[ \Sigma = \text{tril}(UV^\top) + \text{triu}(VU^\top,1), \quad U,V\in\mathbb{R}^{n\times p}. \]

As such we say that \(\Sigma\) is a extended generator representable semiseparable matrix (a EGRSS matrix), giving rise to fast computations. Note that this implicit representation requires only \(O(pn)\) storage and in most cases \(p << n\) meaning that the implicit representation is a very efficient way of storing the full matrix. Furthermore it is shown in (Andersen & Chen 2020) that the Cholesky factorization (and its inverse) of \(\Sigma\) is also implicit represented as

\[ L = \text{tril}(UW^\top,-1) + \text{diag}(d),\quad U,W\in\mathbb{R}^{n\times p},\ d\in\mathbb{R}^n \] \[ L^{-1} = \text{tril}(YZ^\top) + \text{diag}(d)^{-1},\quad Y,Z\in\mathbb{R}^{n\times p},\ d\in\mathbb{R}^n \]

and can be computed in \(O(p^2n)\) operations.

Giving noisy observations we will also need to compute on a variant of EGRSS matrices as seen below

\[ K_y = \text{tril}(UV^\top) + \text{triu}(VU^\top,1) + \text{diag}(d), \quad U,V\in\mathbb{R}^{n\times p},\ d\in\mathbb{R}^n. \]

We call this a extended generator representable quasiseparable matrix (a EGRQS matrix).

using SymEGRSSMatrices, Plots, LinearAlgebra, Optim, Printf, SpecialFunctions, Interact
import SymEGRSSMatrices: spline_kernel
n = 300          # number of samples
σ = 2.0          # noise standard deviation
a,b = -0.2,1.1   # interval [a,b]
δ = b - a

t = a .+ sort(rand(n))*δ;
# FORRESTER ET AL. (2008) FUNCTION
f(t) = (6.0*t .- 2.0).^2 .* sin.(12.0*t .- 4.0)
y = f(t) + σ*randn(length(t));

scatter(t, y, ms=2, label="Observations", xlims=(a,b), xlabel="t") 
plot!(a:δ/n:b, f(a:δ/n:b), label="f(t)",color=:black, ls=:dash,lw=1)

svg

Efficiently Computing Smoothing Splines

The optimality coniditions of the previously mentioned QP is equivalent with solving the following system

\[ \begin{bmatrix} \Sigma + n \lambda I & H \\ H^\top & 0 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} y \\ 0 \end{bmatrix}. \]

For simplicity we set \(K_y = \Sigma + n\lambda I\). From the first equation we have that

\[ K_y c = y - Hd. \]

Inserting this into the second equation we have that

\[ H^\top K_y ^{-1} (y - Hd) = 0 \quad \Rightarrow \quad H^\top K_y ^{-1} H d = H^\top K_y^{-1} y. \]

Given that we can compute \(K_y = LL^\top\) and apply \(L^{-1}\) in \(O(pn)\) operations we see that we can solve the above systems in linear time w.r.t to \(n\).

Note that the above computations i equivalent with fitting a Gaussian process with its kernel matrix equal to \(\Sigma\).

p = 2;
λ = 1e-4;
Ut,Vt = spline_kernel((t' .- a)/(b-a), p);
Σ = SymEGRSSMatrix(Ut*δ^(2p-1),Vt);
H = ones(n,p)
for i = 2:p
  H[:,i] = t.^(p-1)/(factorial(p-1))
end

function smoothing_spline(Σ, H, y, λ)
  n, p = size(H)
  L = cholesky(Σ, n*λ)
  v = L'\(L\y);
  A = (H'*(L'\(L\H)));
  d = A\(H'*v);
  c = L'\(L\(y - H*d));
  log_gml = log(dot(y,c)) + 2.0*logdet(L)/(n-p) + logdet(A)/(n-p);
  return c,d,log_gml
end

c, d, _ = smoothing_spline(Σ, H, y, λ)

scatter(t, y, ms=2, label="Observations", xlims=(a,b), xlabel="t",legend=:topleft) 
plot!(a:δ/n:b, f(a:δ/n:b), label="f(t)",color=:black, ls=:dash,lw=1)
plot!(t, Σ*c + H*d, label="fit",color=:red, lw=2)

svg

Varying the Rougness Penalty

From the first stated optimization problem it is apparant that the parameter \(\lambda\) can be used to emphasize how large the total \(p\)th derivative should be. As such we expect that small values of \(\lambda\) corresponds to an almost complete interpolation of the data, while a large value of \(\lambda\) is equivalent with fitting a \(p-1\) order polynomial.

anim = @animate for λ = [10.0 .^(-10:0.1:0); 10.0 .^(0:-0.1:-10)]
    c, d, _ = smoothing_spline(Σ, H, y, λ);
    p1 = scatter(t, y, ms=2, label="Observations", xlims=(a,b), xlabel="t", legend=false);
    plot!(a:δ/n:b, f(a:δ/n:b), label="f(t)", ls=:dash, color=:black,lw=1)
    plot!(t, Σ*c + H*d, label="fit",color=:red, lw=2, title="λ="*@sprintf("%.3e", λ))
end 
gif(anim, "varying_rougness.gif", fps=10)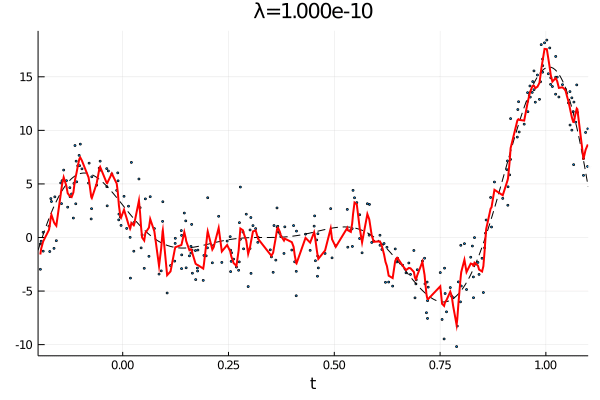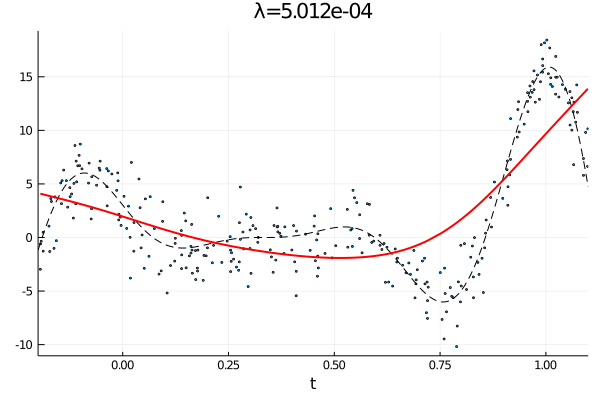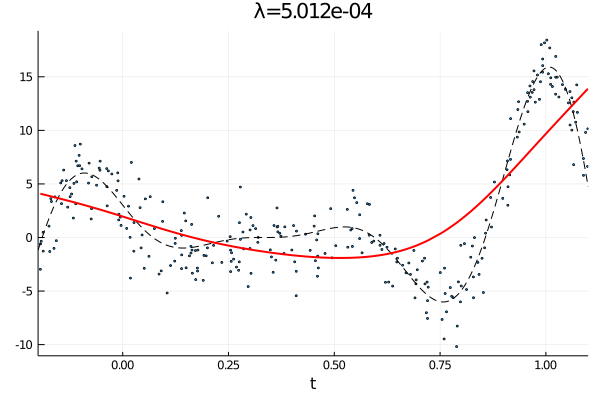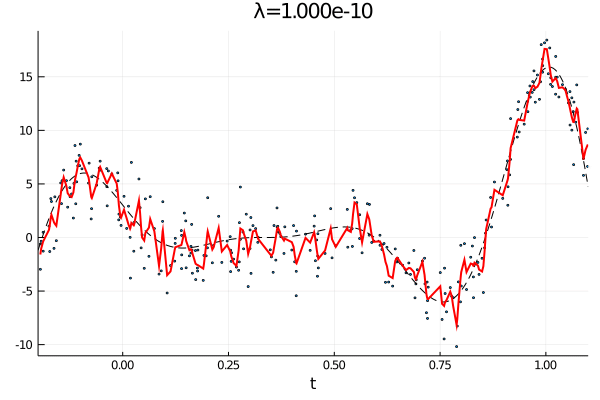

Alt Text

Parameter Selection

Assuming that the measurement errors \(e_i\) are i.i.d Gaussian variables we can estimate the parameters \(\sigma\) and \(\lambda\) using the generalized maximum likelihood function (GML). As stated in (Andersen & Chen 2020) that the GML can be computed as

\[ \log(GML(\lambda)) \propto \log(y^\top\hat{c}) + \frac{1}{n-p}\log|K_y| + \frac{1}{n-p}\log|H^\topK_y^{-1}H|. \]

This function can be efficiently valuated as we can efficiently compute the Cholesky factorization of \(K_y\) and \(H^\topK_y^{-1}H\) is a small matrix. From the optimal \(\hat{\lambda}\) we can compute the optimal standard deviation as

\[ \hat{\sigma}^2 = n\hat{\lambda}\frac{c^\topy}{n-p} \] 
K = SymEGRSSMatrix(Ut*δ^(2p-1),Vt)
function log_gml(v)
  _,_,log_gml = smoothing_spline(K, H, y, 10.0^v);
  return log_gml;
end
res = optimize(log_gml, -10, 0, GoldenSection())
println(res)

λhat = 10.0^res.minimizer;
c, d,_ =  smoothing_spline(K,H,y,λhat)
scatter(t, y, ms=2, label="Observations", xlims=(a,b), xlabel="t", legend=:topleft);
plot!(a:δ/n:b, f(a:δ/n:b), label="f(t)", ls=:dash, color=:black,lw=1)
plot!(t, K*c + H*d, label="fit",color=:red,lw=2,title="λ="* @sprintf("%.2e", λhat))
Results of Optimization Algorithm
     * Algorithm: Golden Section Search
     * Search Interval: [-10.000000, 0.000000]
     * Minimizer: -6.748273e+00
     * Minimum: 7.292673e+00
     * Iterations: 36
     * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true
     * Objective Function Calls: 37

svg

Computing Bayesian Credible Intervals

The standard deviation at prediction \(\hat{y}_i\) is given by

\[ \sigma_i^2 = \hat{\sigma}^2 e_i^\topH(\hat{\lambda})e_i. \]

As such we need to compute the diagonal elements of the influence matrix

\[\begin{aligned} H(\hat{\lambda}) &= I - n \lambda (K_y^{-1} - K_y^{-1} H (H^\top K_y^{-1}H) H^\top K_y^{-1} )\\ &= I - n \lambda L^{-T} (I - L^{-1} H (H^\top K_y^{-1} H) H^\top L^{-T}) L^{-1}\\ &= I - n \lambda L^{-T} (I - Q_1 Q_1^\top ) L^{-1}\\ &= I - n \lambda (K_y^{-1} - (L^{-T} Q_1) (L^{-T} Q_1)^\top). \end{aligned}\]

Where we have used that

\[ L^{-1}H = \begin{bmatrix}Q_1 & Q_2\end{bmatrix} \begin{bmatrix} R \\ 0\end{bmatrix}, \quad Q_1\in\mathbb{R}^{n\times p},\ Q_2\in\mathbb{R}^{n\times (n-p)},\ R\in\mathbb{R}^{p\times p} \]

The diagonal elements of \((L^{-T}Q_1)(L^{-T}Q_1)^\top\) is easily calculated as the row-norms of \(L^{-T}Q_1\). The the same time the diagonal elements of \(K_y^{-1}\) can be efficiently computed using the explicit-implicit representation of \(L^{-1}\). However it should be noted that the algorithm to do so it not nessecarily numerically stable. Hence below we compute the diagonal elements as \(||L^{-1}e_i||_2^2\)

L = cholesky(SymEGRSSMatrix(Ut*δ^(2p-1),Vt), n*λhat)
B = L\H;
F = qr(B);
S = L'\Matrix(F.Q);

dH = zeros(n)
ei = zeros(n);
for i = n: -1 :1
  ei[i] = 1.0;
  dH[i] = norm((L\ei)[i:end])^2
  ei[i] = 0.0;
end

diagH = 1.0 .- n*λhat*(dH - sum(S.*S,dims=2));

The Complete Picture

α = 0.05
β = sqrt(2)*erfinv(1-α)
σhat = sqrt(n*λhat*dot(y,c)/(n-p))

scatter(t, y, ms=2, label="Observations", xlims=(a,b), xlabel="t", legend=false);
plot!(a:δ/n:b, f(a:δ/n:b), label="f(t)", ls=:dash,color=:black,lw=1, ribbon=β*σhat, alpha=0.8, fillalpha=0.1)
plot!(t, K*c + H*d, label="fit",color=:red,lw=2,title="λ="*@sprintf("%.3e", λhat)*", "*  "σ="* @sprintf("%.3e", σhat), ribbon=β*σhat*sqrt.(diagH), fillalpha=0.5)

svg

References

  1. M. S. Andersen and T. Chen, “Smoothing Splines and Rank Structured Matrices: Revisiting the Spline Kernel,” SIAM Journal on Matrix Analysis and Applications, 2020.

© Mikkel Paltorp. Last modified: May 27, 2024. Website built with Franklin.jl and the Julia programming language.