The Matrix Determinant Lemma
In this short note a connection between the determinant of a rank-\(k\) pertubated \(n\times n\) matrix and a \(k\times k\) matrix is explored. We take the approach of (some larger) block matrices which in general can be a good approach to tackle these kind of problems.
Determinants of Block Matrices
We start by stating a very powerful formula regarding the determinat of a block-diagonal matrix. The formula is the basis of everything stated in this note. It is stated without proof as the only proofs I could find was somewhat intricate.
\[ \det\left(\begin{bmatrix}A & B \\ 0 & D\end{bmatrix}\right) = \det(A)\det(D). \]From this it follows that the
\[ \det\left(\begin{bmatrix}A & B \\ C & D\end{bmatrix}\right) = \det(A)\det(D-CA^{-1}B) = \det(D)\det(A - BD^{-1}C). \]We can easily show why this by utilizing (1), the known fact that \(\det(AB)=\det(A)\det(B)\) as well as the following two decomposition
\[ \begin{bmatrix} A & B \\ C & D \end{bmatrix} = \begin{bmatrix} A & 0 \\ C & I_k \end{bmatrix}\begin{bmatrix} I_n & A^{-1}B\\ 0 & D - CA^{-1}B \end{bmatrix} \] \[ \begin{bmatrix} A & B \\ C & D \end{bmatrix} = \begin{bmatrix} I_n & B \\ 0 & D \end{bmatrix}\begin{bmatrix} A-BD^{-1}C & 0\\ D^{-1}C & I_k \end{bmatrix} \]Weinstein–Aronszajn identity
We start by a introducing a special case. Namely the Weinstein-Aronszajn Identity, which explains that the determinant of a identity plus a rank-\(k\) perturbation is equal to the determinant of a \(k\times k\) matrix.
\[ \det( I_n + UV^\top ) = \det(I_k + V^\top U) \]The identity follows straight from (2)
\[ \det\left(\begin{bmatrix} I_n & U\\ V^\top & I_k\end{bmatrix}\right) = \det(I_n)\det(I_k + V^\top I_n^{-1}U) = \det(I_k + V^\top U) \] \[ \det\left(\begin{bmatrix} I_n & U\\ V^\top & I_k\end{bmatrix}\right) = \det(I_k)\det(I_n + UI_k^{-1}V^\top ) = \det(I_n + UV^\top ) \]Visually we can view the identity as 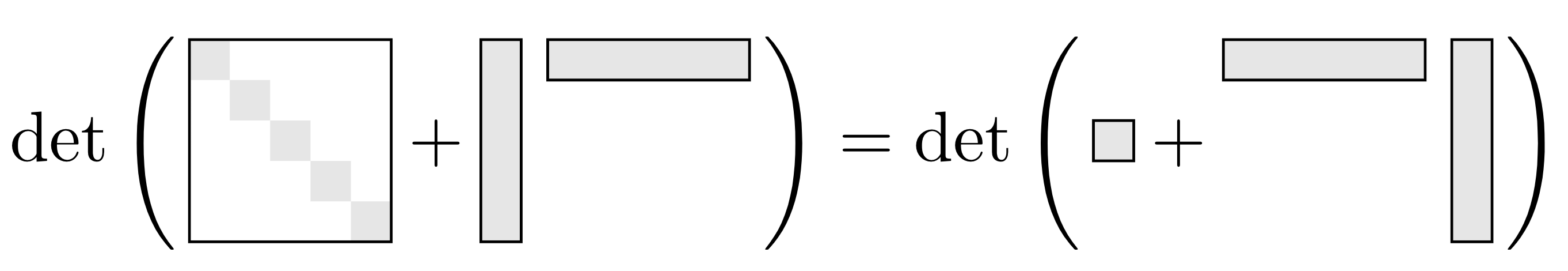
The General Form
The most general form can be stated as
\[ \det(A + UV^\top ) = \det(I_k + V^\top A^{-1} U)\det(A) \]Which explains that the determinant of a \(n\times n\) matrix plus a rank-\(k\) perturbation is equal to the determinant of a \(k\times k\) matrix. This formula follows straight from (2) because we have that
\[ \det\left(\begin{bmatrix} A & U\\ V^\top & I_k\end{bmatrix}\right) = \det(I_k)\det(A + UI_k^{-1}V^\top ) = \det(A + UV^\top ) \]and
\[ \det\left(\begin{bmatrix} A & U\\ V^\top & I_k\end{bmatrix}\right) = \det(A)\det(I_k + V^\top A^{-1}U) = \det(I_k + V^\top A^{-1}U). \]Again we can visually view this as 