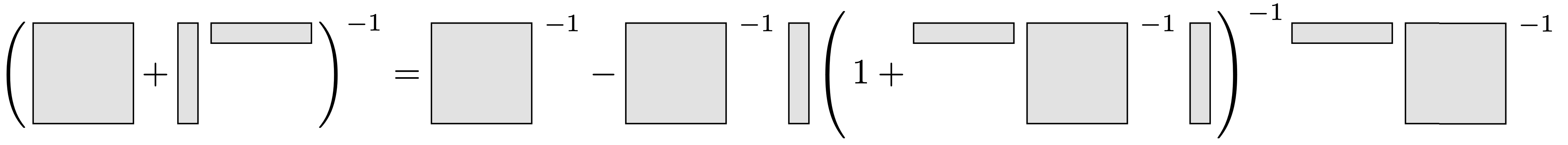The Sherman-Morrison Identity

The Sherman-Morrison identity deals with the inversion of a rank-\(1\) perturbed matrix. In short, it states that its inverse is also a rank-\(1\) perturbed matrix. Most notably it can be used to significantly speed up the computations of the inverse of the total rank-1 perturbed matrix, if the inverse of the pertubed matrix is already known.

A Special Case

The special case of the Sherman-Morrison stated that the inversion of a rank-\(1\) perturbed identity matrix is also a rank-\(1\) perturbed identity matrix.

\[ (I + uv^\top )^{-1} = I - \frac{uv^\top }{1 + v^\top u}\ = I - u(1 + v^\top u)^{-1}v^\top \]

The proof is simple. Assume that the inverse of \((I + uv^\top )\) have a similar form, namely \((I + \alpha uv^\top )\)

\[ (I + uv^\top )(I + \alpha uv^\top ) = I + (uv^\top + \alpha uv^\top + uv^\top \alpha uv^\top ) = I + u(1 + \alpha + v^\top \alpha u)v^\top . \]

Now since needs to be equal to \(I\) for all values of \(u\) and \(v\) we must have the expression inside the parenthesis must be 0 from which we can assert that

\[ \alpha = -(1 + v^\top u)^{-1}. \]

Inserting this into our assumption the formula follows.

The first expression is how the formula is usually stated. However, I like the last form better since it naturally extends to the Sherman-Morrison-Woodbury formula. It also makes it easier to visualize what is doing on

The General Form

We can generalize the formula to a perturbation of a general (invertible) matrix

\[ (A + uv^\top )^{-1} = A^{-1} - \frac{A^{-1}uv^\top A^{-1}}{1 + v^\top A^{-1}u} = A^{-1} - A^{-1}u\left(1 + v^\top A^{-1}u\right)^{-1}v^\top A^{-1}. \]

The intuition behind this is as follows: Set \(B = A + uv^\top \) such that \(B^{-1} = (I + A^{-1}uv^\top )^{-1}A^{-1}\). Then setting \(w = A^{-1}u\) and using the special case it follows.

Again the first expression is how the formula usually is stated, while the second is how I personally like to think of it. Again the formula can be visualized.